|
Abbiamo visto 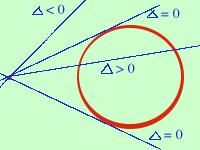 che quando una retta e' tangente ad una circonferenza
ha con essa
2 punti coincidenti in comune,
cioe' facendo il sistema fra la retta e la circonfernza il
discriminante
del sistema e' uguale a zero.
che quando una retta e' tangente ad una circonferenza
ha con essa
2 punti coincidenti in comune,
cioe' facendo il sistema fra la retta e la circonfernza il
discriminante
del sistema e' uguale a zero.Ma allora, se considero il fascio di rette che esce dal punto e fra tutte le rette scelgo quelle che in sistema con la circonferenza hanno il in pratica ho ribaltato la frittata: retta tangente =>
Vediamo di capire meglio il metodo con un esempio pratico: Trovare le tangenti alla circonferenza 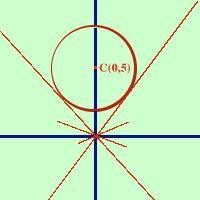 x2+
y2
-10y + 16 = 0
x2+
y2
-10y + 16 = 0
condotte dall'origine O(0,0) E' la circonferenza di centro C(0,5) e raggio 3 e' una circonferenza che abbiamo gia' incontrato Per trovare l'equazione delle rette tangenti considero il fascio di rette con centro l'origine y = mx Faccio il sistema fra la circonferenza ed il fascio di rette y = mx Sostuisco y = mx Calcolo --------- Raccolgo i termini con x2, con x ed i termini noti ed ottengo l'equazione risolvente x2(1 + m2) -10mx + 16 = 0 Ora calcolo il discriminante (delta) b2 - 4ac e lo pongo uguale a zero, in tal modo determino i valori di m per cui le rette del fascio sono tangenti 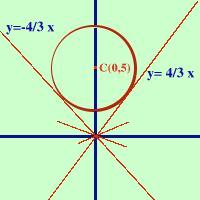 9m2 - 16 = 0
calcoli
9m2 - 16 = 0
calcolim2 = 16/9 m = Le due rette tangenti sono: y = 4/3 x y = -4/3 x vediamo insieme un esercizio |

|

|

|

|