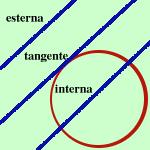
 Una retta rispetto alla circonferenza puo' essere:
Una retta rispetto alla circonferenza puo' essere:
Facendo il sistema fra una retta ed una circonferenza otterremo un'equazione di secondo grado
|

|

|

|

|
 Una retta rispetto alla circonferenza puo' essere:
Una retta rispetto alla circonferenza puo' essere:
Facendo il sistema fra una retta ed una circonferenza otterremo un'equazione di secondo grado
|

|

|

|

|