Equazioni della tangente condotta da un punto sulla circonferenza Se il punto da cui inviare le tangenti si trova sulla circonferenza troveremo solo un'equazione, infatti le tangenti sono due coincidenti: Prova a pensare ad un punto esterno da cui mandi due tangenti ed immagina di avvicinarlo fino ad arrivare alla circonferenza Quindi il metodo sara' esattamente uguale al precedente, in piu' potremo dire che l'equazione che otterremo ponendo il Delta uguale a zero dovra' avere due soluzioni coincidenti, cioe' il primo membro dell'equazione dovra' essere un quadrato perfetto (le soluzioni coincidenti si hanno se e solo se i termini dell'equazione formano un quadrato) Vediamo un esempio pratico Trovare l' equazione della tangente alla circonferenza x2+ y2 - 25 = 0 condotte dal suo punto P(3,4) E' la circonferenza di centro O(0,0) e raggio 5 Per trovare l'equazione della retta tangente considero il fascio di rette passante per il punto P(3,4) y - 4 = m(x - 3) Faccio il sistema fra la circonferenza ed il fascio di rette x2+ y2 - 25 = 0 y = mx -3m + 4 Sostuisco x2+ (mx - 3m + 4)2 - 25 = 0 y = mx - 3m + 4 Calcolo     Formula del quadrato del trinomio x2+ m2x2 + 9m2 + 16 - 6m2x + 8mx - 24m - 25 = 0 ----------------- x2+ m2x2 - 6m2x + 8mx + 9m2 - 24m - 9 = 0 ----------------- Raccolgo i termini con x2, con x ed i termini noti ed ottengo l'equazione risolvente x2(1 + m2) - 2x(3m2 -4m) + 9m2 - 24m - 9 = 0 Ora calcolo il discriminante (anzi il Delta quarti essendo il termine con la x divisibile per 2) (b/2)2 - ac e lo pongo uguale a zero, in tal modo determino i valori di m per cui le rette del fascio sono tangenti a = 1 + m2 b = -2(3m2 - 4m) c = 9m2 - 24m - 9 (b/2)2 - ac = (3m2 - 4m)2 - (1 + m2)(9m2 - 24m - 9) = 0 calcoli 16m2 + 24m + 9 = 0 Come ci aspettavamo e' un quadrato perfetto (4m + 3)2 = 0 4m + 3 = 0             3 m = - ----             4 Sostituisco m nell'equazione del fascio y = mx - 3m + 4 y = (-3/4)x -3(-3/4) + 4 L' equazione della retta tangente e' y = 3  - ---- x 4 25 + ----    4 Vediamo anche un altro metodo che mi ha inviato Daniele: un visitatore del sito Si basa sul fatto che nella circonferenza la tangente in un suo punto e' perpendicolare al raggio nel punto di contatto; Come calcoli e' molto piu' semplice, ma ha il difetto di poter essere usato solo per la circonferenza e solo per la tangente ad un punto sulla circonferenza, mentre l'altro metodo e' generale e si puo' usare anche per tutte le coniche. Trovare l' equazione della tangente alla circonferenza 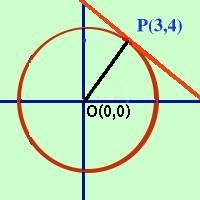x2+ y2 - 25 = 0 condotte dal suo punto P(3,4) calcoliamo il coefficiente angolare della retta OP m = 4 - 0   ------ = 3 - 0 4 --- 3 Quindi la tangente, essendo la perpendicolare avra' coefficiente angolare: m = - 3 --- 4 quindi per trovare la tangente bastera' prendere l'equazione della retta passante per P e con coefficiente angolare uguale a -3/4 y - 4 = - 3 --- 4 (x - 3) moltiplico tutto per 4 per togliere i denominatori 4y - 16 = -3(x-3) 4y - 16 = -3x + 9 4y = -3x + 25 e quindi esplicitando y = 3  - ---- x 4 25 + --- 4