Condizione di perpendicolarita' fra due rette Prima di costruire la formula devo determinare a cosa corrisponde il fatto che due rette siano perpendicolari: per fare questo considero due rette (supponendo che siano perpendicolari) e cerco di trovare una relazione fra i loro coefficienti angolari y = m1x y = m2x 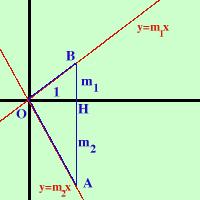Dal punto 1 mando la verticale e ottengo il triangolo OAB Essendo le rette perpendicolari il triangolo OAB e' rettangolo ed ha le misure: OH=1     AH=m2     HB=m1 Poiche' e' rettangolo in esso posso applicare il secondo teorema di Euclide OH2 = AH · HB Sostituendo ai lati le relative misure 1 = m2 · m1 C'e' un piccolo problema: i due valori m1 ed m2 sono uno positivo ed uno negativo, quindi dovremo riscrivere l'uguaglianza come - 1 = m2 · m1 Ricavo m1             1 m1 = - ---               m2 E questa e' la condizione di perpendicolarita' cercata: due rette sono perpendicolari se i loro coefficienti angolari sono opposti ed inversi Opposti vuol dire di segno contrario. Inversi vuol dire che basta rovesciarne uno per ottenere l'altro come ad esempio 3 ed 1/3