|
Per risolvere il problema basta considerare la figura costituita da un triangolo equilatero inscritto in un cerchio: 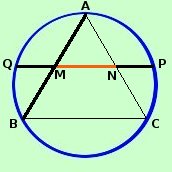 consideriamo poi MN la
congiungente i punti medi di due lati che sara' anche meta' del terzo lato. consideriamo poi MN la
congiungente i punti medi di due lati che sara' anche meta' del terzo lato.Se la sezione aurea e' meta' del lato del triangolo equilatero allora prolungando la congiungente i punti medi sino ad incontrare la circonferenza avro' che il segmento di partenza sara' MP mentre la parte quarta proporzionale sara' QM Infatti per il teorema delle corde applicato alle corde AB e PQ posso scrivere: MP : AM = MB : QM Ma essendo AM = MB = MN MP : MN = MN : QM o meglio, essendo QM = NP MP : MN = MN : NP come volevamo |

|

|

|

|