|
Considero un segmento AB e dal punto B ne traccio la perpendicolare e considero il segmento BO congruente alla meta' di AB 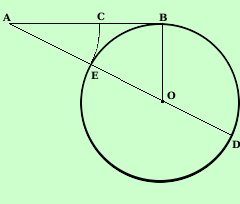 Dal punto O traccio la circonferenza di centro O e raggio BO (meta' di AB) Poi traccio la congiungente il punto A col punto O che incontra la circonferenza in E e D A partire da A riporto il segmento AE su AB: ottengo il segmento AC: AC e' la sezione aurea del segmento AB Per dimostrarlo dobbiamo dimostrare che vale AB : AC = AC : CB Per il teorema della secante e della tangente si ha: AD : AB = AB : AE essendo AE=AC posso scrivere AD : AB = AB : AC Per la proprieta' dello scomporre delle proporzioni posso scrivere (AD-AB) : AB = (AB-AC) : AC Ma AB = 2r = DE e vale anche AD - DE = AE = AC, inoltre AB-AC = CB; quindi AC : AB = CB : AC Applico la proprieta' dell'invertire ed ottengo AB : AC = AC : CB come volevamo Molto piu' semplice e' risolvere il problema inverso: data la sezione aurea trovare il segmento che la genera: lo facciamo nella prossima pagina |

|

|

|

|