Soluzione algebrica E' possibile risolvere il problema della sezione aurea in modo algebrico: lo faremo in questa pagina: 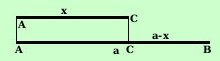Chiamiamo a la lunghezza del segmento e chiamiamo x la misura della sezione aurea del segmento: avremo AB = a___ AC = x___ BC = a-x___ quindi la proporzione AB : AC = AC : CB diventa a : x = x : (a-x) sviluppo la proporzione con la proprieta' fondamentale x2 = a · (a-x) x2 = a2 - ax x2 + ax - a2 = 0 E' un'equazione di secondo grado: la risolvo ed ottengo      Calcoli a (+ 5   - 1) x1 =   2        a (- 5   - 1) x2 =   2 Trattandosi di un problema geometrico la soluzione x2 e' da scartare perche' non abbiamo segmenti negativi (nella geometria euclidea), quindi: AC = x__=   a ( 5   - 1) 2 e radice di 5 e' un numero decimale illimitato non periodico (reale non razionale)