|
Enuncio alcune proprieta' senza dimostrazione Abbiamo che: Dato un qualsiasi poligono regolare e' sempre possibile inscriverlo in una circonferenza 
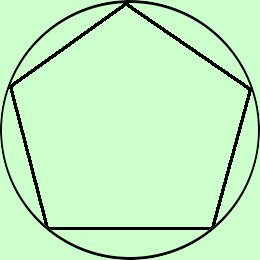
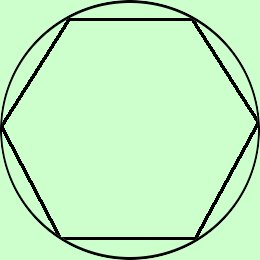ecc...
In questo caso i raggi dei cerchi coincidono con i lati dei triangoli congruenti in cui possiamo suddividere i vari poligoni regolari congiungendo il centro del cerchio circoscritto con i vertici dei poligoni Inoltre avremo che All'aumentare del numero dei lati la misura del perimetro di un poligono regolare inscritto in una circonferenza aumenta avvicinandosi alla misura della lunghezza della circonferenza stess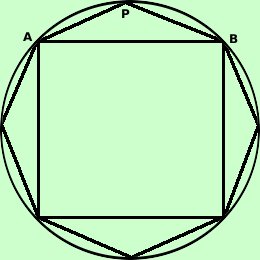a 
Ad esempio se considero il quadrato inscritto e poi l'ottagono regolare
inscritto avremo che il perimetro dell'ottagono e' maggiore del perimetro del
quadrato ma minore della lunghezza della circonferenza:Per mostrare che la misura ciconferenza e' maggiore ddella misura del perimetro di qualunque poligono inscritto basta ricordare che ogni corda e' minore del suo arco Prova a dimostrarlo per esercizio Se considero il lato del quadrato AB ed i lati dell'ottagono AP e PB essi formano il triangolo APB ed in ogni triangolo ogni lato e' minore della somma degli altri due, quindi AB < AP + PB applicandolo a tutti i lati del quadrato e dell'ottagono ottengo la proprieta' |
|
|
|
|