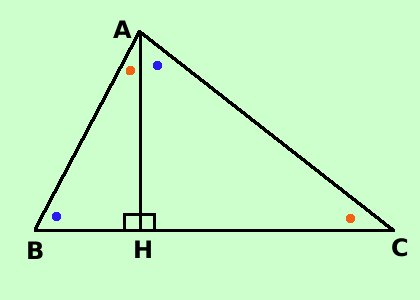
Primo teorema di Euclide In ogni triangolo rettangolo l'altezza relativa all'ipotenusa e' media proporzionale tra le proiezioni dei cateti sull'ipotenusa Utilizziamo il teorema di base: considero i due triangoli ABH e AHC sono simili Metto gli angoli uguali corrispondenti uno sopra l'altro in verticale     A         B         H         C         A         H     ora per scrivere la proporzione prendo due lettere sopra ed in corrispondenza le due lettere sotto: AB : CA = BH : AH = AH : CH In particolare considero BH : AH = AH : CH Come volevamo Da notare che se applichiamo la proprieta' fondamentale delle proporzioni (prodotto dei medi uguale al prodotto degli estremi) otteniamo il risultato del teorema gia' dimostrato nell'equivalenza AH2 = BH · HC