Teorema di base Dato un qualunque triangolo rettangolo, l'altezza relativa all'ipotenusa divide il triangolo in due triangoli simili sia tra loro che con il triangolo dato Prima dimostriamo che sono simili fra loro, poi mostreremo che uno di essi e' simile al triangolo di partenza Prima parte 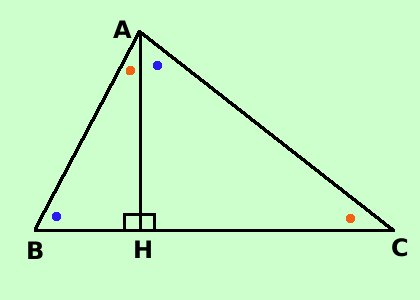Ipotesi: BAC^ = angolo retto AH perpendicolare a BC Tesi: i triangoli BAH ed AHC sono simili Mostriamo che sono triangoli simili, utilizzando il primo criterio di similitudine: Considero i triangoli ABH ed AHC: essi hanno BHA = AHC^ ^perche' angoli retti (per ipotesi) Se sommo l'angolo ABH^ con l'angolo BAH^ ottengo un angolo retto Se sommo l'angolo CAH^ con l'angolo BAH^ ottengo ancora un angolo retto Quindi ABH = CAH^ ^perche' complementari dello stesso angolo (cioe' con lo stesso angolo BAH^formano un angolo retto) Quindi i due triangoli, avendo due angoli congruenti sono simili per il primo criterio di similitudine Come volevamo Seconda parte Dimostriamo ora che uno dei triangoli, ad esempio ABH e' simile al triangolo di partenza ABC, (potrei fare lo stesso ragionamento con AHC quindi entrambe i triangolini sono simili al triangolo di partenza) 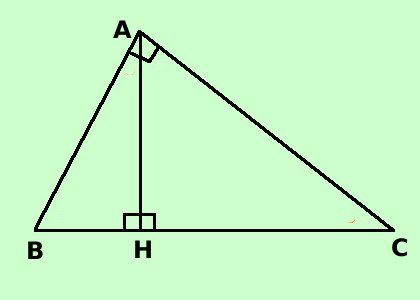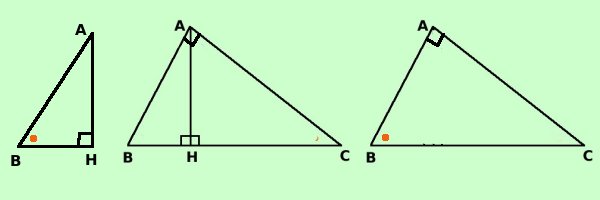Stavolta abbiamo due triangoli in cui uno e' sovrapposto all'altro: se questo ti fa difficolta' puoi sempre pensare di staccare i due triangoli e poi procedere Ipotesi: BAC^ = angolo retto AH perpendicolare a BC Tesi: i triangoli ABH ed ABC sono simili Mostriamo che sono triangoli simili, utilizzando il primo criterio di similitudine: Considero i triangoli ABH ed ABC: essi hanno ABH = ABC^ ^perche' angoli coincidenti AHB = BAC^ ^perche' retti per ipotesi Quindi i due triangoli, avendo due angoli congruenti sono simili per il primo criterio di similitudine Come volevamo