Primo criterio di similitudine fra triangoli Se due triangoli hanno due angoli congruenti allora i due triangoli sono simili 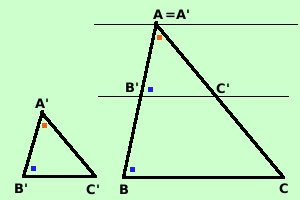Ipotesi      BAC = B'A'C'^ ^ ABC = A'B'C'^ ^ Tesi     BCA = B'C'A'^ ^ AB : A'B' = BC : B'C' = AC : A'C' Intanto possiamo dire che i triangoli, avendo due angoli coingruenti avranno congruenti anche il terzo angolo per un teorema precedente; resta quindi da dimostrare che i lati corrispondenti sono in proporzione Trasporto il triangolo B'A'C' sul triangolo BAC in modo che l'angolo A' coincida con l'angolo A, in questo modo i lati BC e B'C', tagliati dalla trasversale AC, hanno angoli corrispondenti uguali e quindi sono paralleli, ma allora ci troviamo nelle condizioni del teorema di Talete e possiamo dire che vale AB : A'B' = AC : A'C' 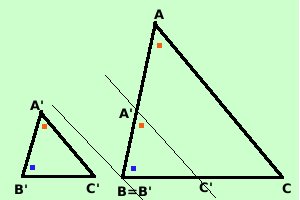Per dimostrare l'altra parte della proporzione basta sovrapporre i triangoli facendo coincidere l'angolo B' con l'angolo B Replicando lo stesso ragionamento otteniamo: AB : A'B' = BC : B'C' Come volevamo