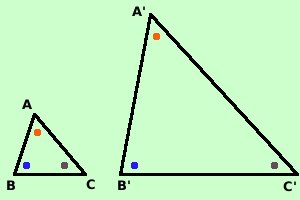
Similitudine fra triangoli Intuitivamente possiamo dire che la similitudine e' una corrispondenza fra figure che conserva la forma ma non l'estensione: pensa al cinematografo ed allo schermo: ponendo lo schermo a differenti distanze otterremo figure simili ma di dimensioni diverse; nella similitudine si conserveranno uguali gli angoli delle varie figure in corrispondenza, e quindi, per il teorema di Talete, avremo che le varie misure di grandezze corrispondenti saranno in proporzione Diremo: Due triangoli si dicono simili se hanno gli angoli ordinatamente uguali ed i lati opposti a tali angoli in proporzione ABC simile ad A'B'C' equivale a Angoli A=A' B=B' C=C' ed inoltre AB:A'B'=BC:B'C'=CA:C'A' Ordinatamente significa che se il perimetro di un triangolo ABC e' percorso in senso antiorario, allora anche il triangolo simile A'B'C' sara' percorso in senso antiorario E' importante sottolineare che i lati opposti ad angoli conguenti si corrisponderanno nella proporzione e viceversa gli angoli opposti a lati proporzionali sono congruenti fra loro Naturalmente e' piuttosto complicato, dati due triangoli, controllare che i tre angoli siano uguali e i lati corrispondenti siano in proporzione, pertanto utilizzeremo dei criteri che ci permetteranno di verificare la similitudine con un numero ridotto di elementi in corrispondenza: Nelle prossime pagine vedremo 3 criteri che saranno fondamentali per lo studio della similitudine (e quindi da sapere molto bene) Ti ricordo che un criterio e' una "scorciatoia" che ci permette di ottenere un risultato in modo abbreviato senza dover applicare tutti i passaggi