Secondo criterio di similitudine fra triangoli Se due triangoli hanno due lati proporzionali e gli angoli compresi uguali allora i due triangoli sono simili 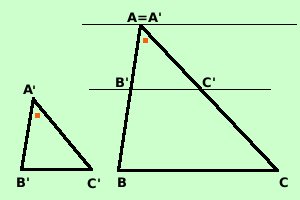Ipotesi      AB : A'B' = AC : A'C' BAC = B'A'C'^ ^ Tesi BCA = B'C'A'^ ^ ABC = A'B'C'^ ^ AB : A'B' = BC : B'C' Trasporto il triangolo B'A'C' sul triangolo BAC in modo che l'angolo A' coincida con l'angolo A, in questo modo il lato A'B' va sopra AB ed il lato A'C' va sopra AC. Traccio per A la retta parallela alla retta B'C'; siccome vale AB : A'B' = AC : A'C' per il teorema inverso del teorema di Talete la retta BC e' parallela alla retta B'C', ed avremo: BCA = B'C'A'^ ^ perche' angoli corrispondenti rispetto alle rette parallele B'C' e BC tagliate dalla trasversale AC ABC = A'B'C'^ ^ perche' angoli corrispondenti rispetto alle rette parallele B'C' e BC tagliate dalla trasversale AB Quindi i due triangoli hanno tutti e tre gli angoli uguali e per il primo criterio sono simili, come volevamo