Angoli al centro ed alla circonferenza Questo e' uno di quei teoremi fondamentali che devi sapere sia enunciare che dimostrare: i teoremi fondamentali in geometria si possono contare sulle dita di una mano: per gli altri teoremi di solito e' sufficiente sapere che esistono, cioe' conoscerne l'enunciato, per poterli applicare alla soluzione di problemi. 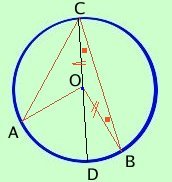Nei teoremi fondamentali e' invece essenziale conoscere bene anche la dimostrazione Teorema In ogni circonferenza l'angolo al centro e' doppio dell'angolo alla circonferenza che insiste sullo stesso arco insistere sullo stesso arco significa che il loro arco e' lo stesso ipotesi    AOB^= Angolo al centro ACB^angolo alla circonferenza tesi AOB^= 2ACB^    Dimostrazione Traccio il diametro COD Dividiamo la dimostrazione in due parti: prima dimostriamo che DOB^=  2DCB^ e poi dimostreremo che anche DOA^=  2DCA^ Considero il triangolo OCB, esso e' isoscele perche' OC ed OB sono raggi, quindi i due angoli OCB^ed OBC^sono congruenti. L'angolo DOB^e' un angolo esterno rispetto al triangolo OCB ed e' quindi congruente alla somma dei due angoli interni non adiacenti; siccome i due angoli sono congruenti ne segue che DOB^= 2OCB^come volevamo Lascio a te per esercizio la dimostrazione relativa alla seconda parte Vediamo nelle prossime pagine alcune precisazioni su questo teorema ed anche alcune conseguenze Ancora sul teorema Precisazioni sugli angoli alla circonferenza Teorema cosiddetto di "Dante"