|
Talvolta, o per far capire meglio l'alunno che ha qualche difficolta' o per costringere a ragionare l'alunno piu' "secchione", il docente presenta la figura dell'angolo al centro ed alla circonferenza in modo alternativo; vediamo in questa pagina quali casi si possono presentare 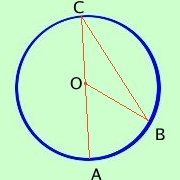 1 per l'alunno con qualche difficolta' conviene presentare il teorema in modo semplificato considerando un lato dell'angolo alla circonferenza coincidente con il diametro in questo modo non c'e' bisogno di suddividere la dimostrazione in due parti 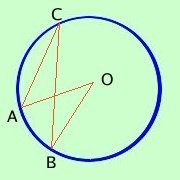 2 per l'alunno piu' preparato presentando la figura come qui a lato (si deve dimostrare che AOB^= 2ACB^) si costringe l'alunno a ragionare ed a costruire una figura che faccia riferimento alla differenza fra gli angoli invece che alla somma 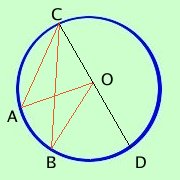 a sinistra vedi come costruire la figura: considera il diametro passante per C ed O; l'angolo che avevi e' ora la differenza fra due angoli AOB^= AOD^- BOD^ e devi considerare i triangoli AOC e BOC |

|

|

|

|