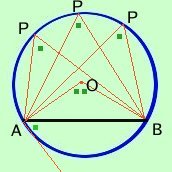
Conseguenza immediata del teorema sugli angoli al centro ed alla circonferenza e' che: Tutti gli angoli alla circonferenza che insistono sullo stesso arco sono congruenti infatti sono tutti congruenti alla meta' dello stesso angolo al centro inoltre anche l'angolo formato da AB con la tangente alla circonferenza in A ed in B e' un angolo alla circonferenza che insiste sull'arco AB Veramente l'angolo formato da AB con la tangente alla circonferenza e' la posizione limite dell'angolo alla circonferenza: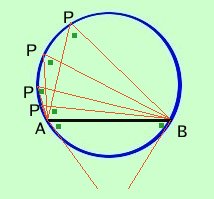 
pensa al triangolo PAB e fai tendere il punto P ad A facendolo scorrere sulla circonferenza: l'angolo APB^ restera' sempre la meta' dell'angolo al centro anche se il lato AP diventa piccolissimo; ti ricordo che l'angolo e' la parte di piano limitata da due semirette aventi la stessa origine, ed anche se il punto P e' a pochi millesimi di millimetro da A puoi sempre pensare le semirette uscenti da P e che si appoggiano su PA e su PB; siccome l'angolo resta sempre congruente , allora sara' congruente anche l'angolo in posizione limite, compreso fra la corda AB e la tangente in A alla circonferenza il segmento PA diventera' sempre piu' vicino alla tangente e nella posizione limite sara' esattamente sulla tangente |
|
|
|
|