|
Consideriamo in nero un sistema di coordinate in cui il punto P abbia coordinate (che chiameremo vecchie coordinate) P = (x,y) Consideriamo poi in rosso un altro sistema di coordinate in cui il punto P sara' individuato da (nuove coordinate) P = (X,Y) 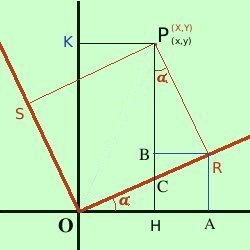 Sappiamo inoltre che i nuovi assi
sono ruotati attorno all'origine rispetto ai vecchi assi dell'angolo
Sappiamo inoltre che i nuovi assi
sono ruotati attorno all'origine rispetto ai vecchi assi dell'angolo Allora osserva la figura: dobbiamo trovare il segmento OH (x) utilizzando le nuove coordinate X e Y calcoleremo OH come differenza fra OA ed AH Considerando il triangolo OAR per i teoremi sui triangoli rettangoli in trigonometria abbiamo OA = OR cos Ora considero il triangolo PBR essendo BR = HA; l'angolo BPR vale per i teoremi sui triangoli rettangoli in trigonometria abbiamo AH = BR = PR sen quindi abbiamo OH = OA - AH = X cos quindi posso scrivere x = X cos Troviamo la formula equivalente per la y Osserva la figura a destra: dobbiamo trovare il segmento OK (y) utilizzando le nuove coordinate X e Y 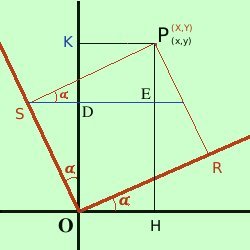 calcoleremo
OK come somma fra
OD e
DK
calcoleremo
OK come somma fra
OD e
DKConsiderando il triangolo ODS per i teoremi sui triangoli rettangoli in trigonometria abbiamo OD = OS cos Ora considero il triangolo PES essendo PE = KD; l'angolo PSE vale per i teoremi sui triangoli rettangoli in trigonometria abbiamo KD = PE = PS sen quindi abbiamo OK = OD + DK = X sen quindi posso scrivere y = X sen Poiche' negli esercizi dovremo sostituire le nuove coordinate alle vecchie conviene considerare solamente le formule con prima dell'uguale le vecchie coordinate; non conviene ricavare le formule inverse anche per la complessita' dei calcoli Raccogliendo, le equazioni per la rotazione di coordinate saranno
sapendo che sen
Come esercizio dimostriamo che l'equazione dell'iperbole equilatera x2 - y2 = a2 con una rotazione di 45° si trasforma nell'equazione dell'iperbole equilatera riferita ai propri assi XY = K soluzione |

|

|

|

|