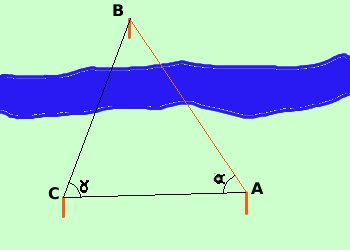
Distanza fra due punti visibili ma uno non accessibile Supponiamo di voler calcolare la distanza fra due punti A e B: io mi trovo in A ma non posso raggiungere B perche' e' al di la' del fiume Possiamo spostarmi in un punto C e calcolare la distanza AC ed inoltre gli angoli ACB e CAB Abbiamo quindi il triangolo ABC in cui conosciamo due angoli ed i l lato compreso, quindi per risolvere il triangolo possiamo calcolare il terzo angolo ricordando che la somma degli angoli interni di un triangolo e' un angolo piatto = 180° - - e poi applicare il teorema dei seni AC    ---------  = sen AB --------- sen e quindi ottenere AB = AC sen ---------------- sen Vediamo anche qui un esercizio supponiamo di spostarci dal punto A di 20 metri AC = 20 m calcolo gli angoli (con il teodolite) Nota: questo e' un esercizio teorico e quindi considero numeri semplici: se calcoli effettivamente gli angoli nella realta' troverai anche primi e secondi e quindi i calcoli saranno molto piu' complicati BAC = = 80° BCA = = 60° e quindi per differenza = ABC = 180°-80°- 60° = 40° AB = 20 sen 60° ---------------- sen 40° 20·0,87 = ---------------- = 0,64 26,9 m