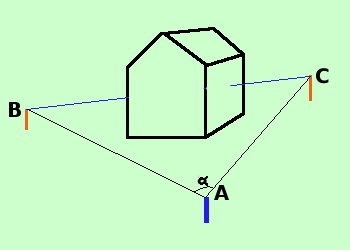
Supponiamo di voler calcolare la distanza fra due punti B e C ma che fra essi ci sia un ostacolo (nella figura una specie di casetta) Possiamo calcolare le distanze AB e AC ed inoltre l'angolo BAC Per calcolare AB ed AC possiamo usare un decametro a nastro e per misurare l'angolo si usa un teodolite (in futuro fare link) Abbiamo quindi il triangolo ABC in cui conosciamo due lati e l'angolo compreso, quindi per calcolare il terzo lato possiamo usare, ad esempio, il teorema di Carnot BC2 = AB2 + AC2 - 2·AB·AC cos 
quindi BC =  (AB2 + AC2 - 2·AB·AC
cos
)
Vediamo un esercizio supponiamo di avere AB = 20 m AC = 30 m BAC = 120° BC =  ( 202
+ 302 - 2·20·30·cos
120°) = [400 + 900 -
1200·(-0,5)]= 1900 = 43,6
m
|
|
|
|
|