Bisettrici di un triangolo
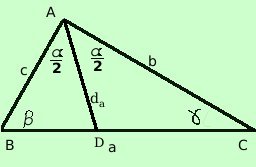
Per calcolare il valore della bisettrice AD dell'angolo  cacoliamo le aree dei due
triangoli ADB e ADC in cui il triangolo ABC viene diviso
dalla bisettrice. cacoliamo le aree dei due
triangoli ADB e ADC in cui il triangolo ABC viene diviso
dalla bisettrice.
Ponendo poi che la somma delle aree dei due triangoli ADB e ADC
equivale all'area del triangolo ABC potremo trovare il valore
da della bisettrice
Area del triangolo ADB
Area del triangolo ADC
Area del triangolo ABC
| As(ABC) = |
1

2
|
b c sen
|

|
Essendo
As(ADC) + As(ADB) = As(ABC)
avremo
1

2
|
c da sen
|


2
|
1
+ 
2
|
b da sen
|


2
|
1
= 
2
|
b c sen
|

|
moltiplico tutti i termini per 2 ed ottengo
| c da sen
|


2
|
+ b da sen
|


2
|
= b c sen
|

|
Ora raccolgo da
Ricavo da
| da =
|
b c sen

|
|

|
|
| (b + c) sen
|
 /2 /2
|
Per la formula di duplicazione so
che
sen  = 2 sen = 2 sen  /2 cos /2 cos  /2 /2
| da =
|
2 b c sen
 /2 cos /2 cos  /2 /2

(b + c) sen
 /2 /2
|
Semplifico ed ottengo la formula finale
|
da =
|
2 b c cos  /2 /2

b + c
|
e quindi, ricavando le varie bisettrici da,
db, dc, avremo le formule
|
da =
|
2 b c cos  /2 /2

b + c
|
|
db =
|
2 a c cos 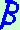 /2 /2

a + c
|
|
dc =
|
2 a b cos  /2 /2

a + b
|
|




