 Consideriamo l'angolo di 18 gradi: se lo ribalto attorno all'asse
delle x ottengo un angolo di 36 gradi, cioe' un decimo
dell'angolo giro, allora la corda dell'arco e' il lato del
decagono regolare.
Consideriamo l'angolo di 18 gradi: se lo ribalto attorno all'asse
delle x ottengo un angolo di 36 gradi, cioe' un decimo
dell'angolo giro, allora la corda dell'arco e' il lato del
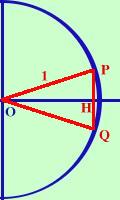
decagono regolare.Dalla geometria si sa che il lato del decagono regolare e' la sezione aurea del raggio Calcolo quindi la lunghezza del segmento PQ PQ = x Raggio : PQ = PQ : (raggio-PQ) 1 : x = x : (1 - x) ottengo l'equazione Calcoli x2 + x - 1 = 0 che mi da' come unica soluzione accettabile -1 + x = ---------- = PQ 2 e quindi essendo PH la meta' di PQ -1 + PH = ---------- 4
PH2 + OH2 = OP2 Ricavo OH Calcoli
Per trovare la tangente faccio seno fratto coseno e, dopo laboriosi calcoli per razionalizzare, ottengo
|

|

|

|

|