Area del cerchio Facciamo ora per l'area del cerchio l'equivalente di quanto fatto per la lunghezza della circonferenza 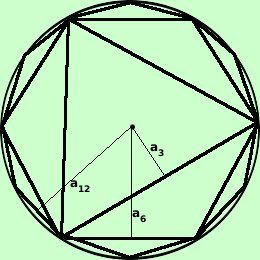Considero una circonferenza di raggio r e considero l'area di tutti i poligoni regolari in essa inscritti In figura, per semplicita' di rappresentazione, ne considero solo alcuni, ma tu devi pensarli tutti La misura dell'Area di tali poligoni (perimetro per apotema diviso due o meglio semiperimetro per apotema) aumentera' all'aumentare del numero dei lati e si avvicinera' indefintamente al valore dell' area della circonferenza, che chiameremo per ora As Chiamando 2p il perimetro e quindi p il semiperimetro e chiamando a le apoteme avremo che le aree sono p3·a3 area del triangolo equilatero inscritto p3·a3 area del quadrato inscritto p3·a3 area del pentagono regolare inscritto p3·a3 area dell'esagono regolare inscritto p3·a3 area dell'ettagono regolare inscritto ............................. ............................. Avremo: p3·a3 < p4·a4 < p5·a5 < p6·a6 < p7·a7 < ......< As C'e' da dire subito che all'aumentare del numero dei lati le apoteme dei poligoni inscritti si avvicinano sempre piu' al valore del raggio r 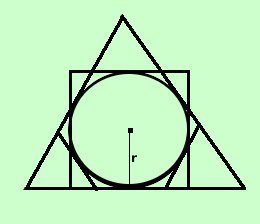Considero poi anche tutti i poligoni regolari circoscritti In figura, per semplicita' di rappresentazione, ne considero solo alcuni, ma tu devi pensarli tutti L'area di tali poligoni (perimetro per raggio diviso due, perche' l'apotema coincide con il raggio) diminuira' all'aumentare del numero dei lati e si avvicinera' indefinitamente al valore dell'area del cerchio Chiamando 2p il perimetro e quindi p il semiperimetro avremo per le aree di poligoni regolari circoscritti p3r area del triangolo equilatero circoscritto p4r area del quadrato circoscritto p5r area del pentagono regolare circoscritto p6r area dell'esagono regolare circoscritto p7r area dell'ettagono regolare circoscritto ............................. ............................. Avremo: p3r > p4r > p5r > p6r > p7r > ......> As Quindi, raccogliendo, per l'area del cerchio potremo scrivere p3a3 <p3a3 <p3a3 <p3a3 <p3a3 < ......< As <.......<p7r <p6r <p5r <p4r <p3r Ora le due classi di aree dei poloigoni inscritti e circoscritti formano due classi contigue di numeri perche': Sono classi separate: ogni area di poligono regolare inscritto e' minore di ogni area di poligono regolare circoscritto Godono dell'avvicinamento indefinito: dato un numero piccolo a piacere posso trovare un'area di poligono regolare circoscritto ed un'area di poligono regolare inscritto tali che la loro differenza sia minore del numero fissato (basta aumentare sufficientemente il numero dei lati) Le due classi contigue individuano un unico elemento separatore cioe' l'area del cerchio, come volevamo Visto che abbiamo trovato le aree dei poligoni facendo perimetro per apotema diviso 2, potremo applicare il metodo anche al cerchio considerando la circonferenza come un poligono di infiniti lati: avremo che il perimetro coincide con la lunghezza della circonferenza e l'apotema coincide con il raggio, quindi As cerchio =   2 r ---------- 2 · r = r2 L'area del cerchio si ottiene moltiplicando il valore di pi greco per il quadrato del raggio Problema Trovare l'area del cerchio di raggio r = 5 cm Soluzione Ascerchio = r2 = ·52 = ·25 =25 cm2 Data l'importanza dell'argomento lo ripeto ancora: questo e' il valore matematico dell'area del cerchio il fatto che vale all'incirca 78 cm2 (25 · 3,14..) ti deve essere noto, ma non deve essere scritto nello svolgimento del problema