|
Ora individuiamo, in modo matematico, il valore della lunghezza della circonferenza  Considero una circonferenza di raggio r e ne considero tutti i poligoni regolari inscritti In figura, per semplicita' di rappresentazione, ne considero solo alcuni, ma tu devi pensarli tutti La misura del perimetro (chiamiamolo 2p) di tali poligoni aumentera' all'aumentare del numero dei lati e si avvicinera' indefintamente al valore della lunghezza della circonferenza, che, in accordo con la pagina precedente, chiameremo 2 Chiamando tali perimetri di poligoni regolari inscritti 2pi3 perimetro del triangolo equilatero inscritto 2pi4 perimetro del quadrato inscritto 2pi5 perimetro del pentagono regolare inscritto 2pi6 perimetro dell'esagono regolare inscritto 2pi7 perimetro dell'ettagono regolare inscritto ............................. ............................. Avremo: 2pi3 < 2pi4 < 2pi5 < 2pi6 < 2pi7 < ......< lunghezza circonferenza= 2 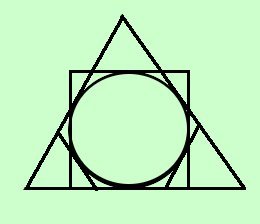 Considero poi anche tutti i poligoni regolari circoscritti In figura, per semplicita' di rappresentazione, ne considero solo alcuni, ma tu devi pensarli tutti La misura del perimetro di tali poligoni diminuira' all'aumentare del numero dei lati e si avvicinera' indefinitamente al valore della lunghezza della circonferenza Chiamando tali perimetri di poligoni regolari circoscritti 2pc3 perimetro del triangolo equilatero circoscritto 2pc4 perimetro del quadrato circoscritto 2pc5 perimetro del pentagono regolare circoscritto 2pc6 perimetro dell'esagono regolare circoscritto 2pc7 perimetro dell'ettagono regolare circoscritto ............................. ............................. Avremo: 2pc3 > 2pc4 > 2pc5 > 2pc6 > 2pc7 > ......> lunghezza circonferenza= 2 Quindi, raccogliendo, per la lunghezza della circonferenza potremo scrivere 2pi3 <2pi4 <2pi5 <2pi6 <2pi7 < ......< 2 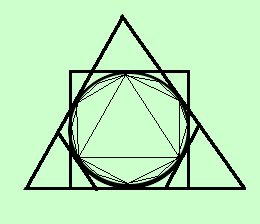 Ora le due classi di perimetri inscritti e circoscritti formano due classi contigue di numeri perche':
Misura lunghezza circonferenza = 2 Visto il ragionamento fatto a volte si dice anche che la circonfernza e' il poligono regolare con un numero infinito di lati |

|

|

|

|