|
Cerchiamo, intuitivamente di capire quanto "grosso modo" puo' misurare la circonferenza di raggio dato r 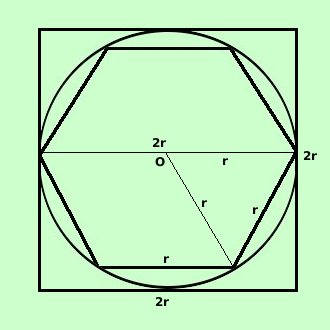 Considero una circonferenza di raggio r e ne considero l'esagono regolare inscritto e il quadrato circoscritto. Il quadrato ha il lato di misura 2r essendo tale lato congruente al diametro della circonferenza. Quindi avremo che il perimetro del quadrato vale Perimetro = 2p = 4 · 2r = 8r L'esagono regolre inscritto in una circonferenza ha il lato congruente al raggio della circonferenza stessa Pertanto l'esagono avra' perimetro di misura Perimetro = 2p = 6 · r = 6r La circonferenza avra una lunghezza che dipendera' dal suo diametro (se varia il diametro varia anche la circonferenza) chiamiamo tale lunghezza Misura circonferenza = numero · 2r e la misura della circonferenza sara' minore del perimetro del quadrato ma maggiore del perimetro dell'esagono 6r < numero · 2r <8r divido tutti i termini di questa disuguaglianza per 2r cioe' per il diametro vedi teoria della misura: equivale a dire "misuro la circonferenza rispetto al suo diametro" ottengo 3 < numero < 4 Quindi la misura della circonferenza rispetto al suo diametro e' un numero compreso fra 3 e 4: Tale numero, per convenzione, verra' chiamato pi greco e, per indicarlo, verra' utilizzato il simbolo 3 < Ed indicheremo la misura della lunghezza della circonferenza come Misura circonferenza = 2 |

|

|

|

|