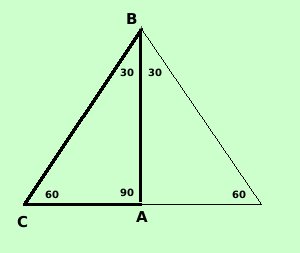
 E' logicamente un triangolo rettangolo poiche' ha un angolo di 90°;
inoltre e' la meta' di un triangolo equilatero: infatti eseguendo un
ribaltamento attorno al cateto maggiore ottengo un triangolo con tre angoli di
60°, cioe' equiangolo e quindi equilatero
E' logicamente un triangolo rettangolo poiche' ha un angolo di 90°;
inoltre e' la meta' di un triangolo equilatero: infatti eseguendo un
ribaltamento attorno al cateto maggiore ottengo un triangolo con tre angoli di
60°, cioe' equiangolo e quindi equilateroAnche in questo triangolo basta conoscere almeno un lato (cateto o ipotenusa) per risolvere il triangolo Per i lati avremo che, chiamata l l'ipotenusa BC avremo che CA e' meta' del lato del triangolo equilatero quindi vale l/2 cateti e siccome vale il teorema di Pitagora possiamo trovare l'altro cateto h: BC2 = AC2 + AB2 l2 = (l/2)2 + h2 h2 = l2 - (l2/4) h2 = 3l2/4 h = Porto fuori di radice i quadrati ed ottengo
quindi essendo noto il valore l dell'ipotenusa BC avremo CA = l/2
Essendo invece noto il valore h del cateto AB avremo
Razionalizzo ed ottengo
Quindi
|

|

|

|

|