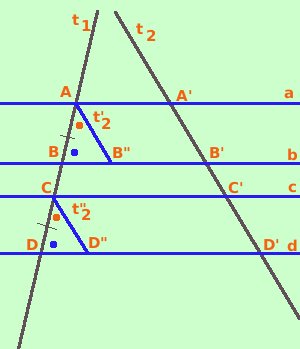
Conservazione dell'uguaglianza Dimostriamo che a segmenti uguali sulla prima trasversale corrispondono segmenti uguali sulla seconda trasversale So per ipotesi che le rette a, b, c, d sono parallele, devo dimostrare che se i segmenti formati sulla prima retta sono uguali fra loro allora anche i segmenti formati sulla seconda retta sono uguali fra loro se AB = CD allora A'B' = C'D' Ipotesi a // b // c // d AB = CD             Tesi A'B' = C'D' Dimostrazione: Dal punto A traccio la parallela a t2 che taglia la retta b in B" Dal punto C traccio la parallela a t2 che taglia la retta d in D" La figura A B" B' A' avendo i lati opposti due a due paralleli e' un parallelogramma e quindi AB"=A'B' La figura C D" D' C' avendo i lati opposti due a due paralleli e' un parallelogramma e quindi CD"=C'D' quindi per dimostrare che A'B'=C'D' bastera' dimostrare che sono uguali i triangoli ABB" e CDD" Essi hanno AB = CD per ipotesi BAB" = DCD" ^         ^ perche' angoli corrispondenti rispetto alle parallele t'2 e t"2 tagliate dalla trasversale t1 ABB" = CDD" ^         ^ perche' angoli corrispondenti rispetto alle parallele b e d tagliate dalla trasversale t1 Quindi per il secondo criterio di congruenza i due triangoli sono congruenti ed in particolare AB"=CD" Poiche' AB"=A'B' e CD"=C'D' segue A'B'=C'D' come volevamo dimostrare