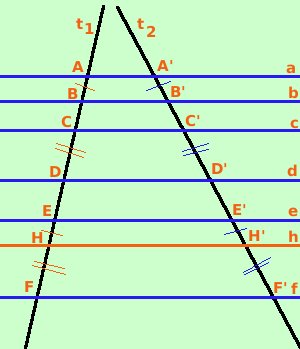
Dimostriamo che si conserva la somma, cioe' se EF e' la somma di AB e CD allora E'F' e' la somma di A'B' e C'D' Sarebbe a dire: Alla somma di segmenti sulla prima trasversale corrisponde, sulla seconda trasversale, la somma dei segmenti corrispondenti So per ipotesi che le rette a, b, c, d, e, f sono parallele, devo dimostrare che se vale EF = AB + CD allora vale anche E'F' = A'B' + C'D'
Dimostrazione: Scelgo la retta del fascio h in modo che EH = AB, di conseguenza HF = CD Per le dimostrazione precedente essendo EH = AB sara' anche E'H' = A'B' Per le dimostrazione precedente essendo HF = CD sara' anche H'F' = C'D' Quindi tutto E'F' = E'H'+ H'F' = A'B' + C'D' come volevamo dimostrare |

|

|

|

|