Grandezze incommensurabili Mostriamo come prima cosa che esistono segmenti incommensurabili, cioe' per cui non e' possibile trovare nessuna sottomultipla comune: lo vedremo sul lato e la diagonale del quadrato Teorema La diagonale ed il lato di un quadrato sono fra loro incommensurabili 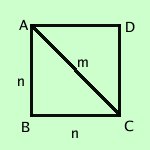ipotesi     ABCD quadrato     tesi    AC__ -----    AB__ m   -----      n la tesi significa che non posso trovare nessuna sottomultipla comune e quindi il rapporto fra AC ed AB non potra' essere espresso come rapporto di due numeri m ed n Facciamo la dimostrazione per assurdo: supponiamo che esista una sottomultipla per cui AC valga m ed AB valga n; mostriamo che otteniamo un risultato impossibile se AC__= m   ed  AB__= n   per il teorema di Pitagora applicato al triangolo rettangolo ABC avremo m2 = n2 + n2 cioe' m2 = 2 n2 Ora esistono due teoremi sulla scomposizione di un numero in fattori primi che ci mostrano che questa uguaglianza e' impossibile Primo: se due numeri sono uguali allora hanno la stessa scomposizione in fattori primi Secondo: se un numero e' elevato al quadrato allora tutti i suoi fattori primi compaiono un numero pari di volte   sarebbe a dire che tutti i fattori primi sono a potenze 2 o 4 o 6 eccetera; ad esempio 144 che e' il quadrato di 12 si scompone come 24 ·32 Osserviamo l'uguaglianza m2 = 2 n2 I due termini prima e dopo l'uguale devono avere gli stessi fattori primi e nello stesso numero Il fattore 2 nel primo termine, essendo questo un quadrato deve esservi un numero pari di volte: 2 oppure 4 oppure 6... Il fattore 2 nel secondo termine, internamente ad n2 dovra' comparire un numero pari di volte cioe' 2 o 4 o 6... pero' c'e' anche il 2 fuori di n2 e quindi dopo l'uguale il fattore 2 compare un numero dispari di volte quindi l'uguaglianza non e' vera ed il teorema e' dimostrato: i segmenti AC e AB sono tra loro incommensurabili Diremo che due grandezze sono incommensurabili se non hanno nessuna sottomultipla comune sara' a dire che la misura non potra' essere espressa da un numero razionale; per poter procedere quindi avremo bisogno di un nuovo tipo di numeri che ci permettano di superare l'ostacolo: i cosiddetti Numeri Reali Non prendere questo teorema troppo alla leggera: e' il responsabile della morte di una grande civilta' (nota storica)