|
Vale il teorema Un parallelogramma e' equivalente ad un triangolo avente come base la stessa base e per altezza il doppio dell'altezza del parallelogramma
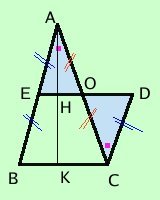 Sovrapponiamo le basi e, siccome il triangolo ABC ha il doppio dell'altezza del parallelogramma EBCD per il teorema ingenuo di Talete avremo che (essendo H il punto medio di AK) i punti E ed O sono punti medi dei lati AB ed AC del triangolo ABC. Considero i triangoli AEO e OCD essi hanno:
Infatti, considero il quadrilatero EBCO, se vi aggiungo il triangolo AEO ottengo il triangolo ABC, se invece vi aggiungo il triangolo ODC ottengo il parallelogramma EBCD NOTA 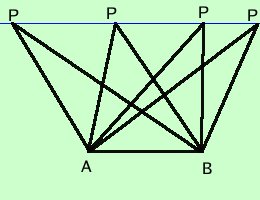 Come conseguenza avremo
che tutti i triangoli aventi congruenti la base e l'altezza sono tra loro equivalenti:
Come conseguenza avremo
che tutti i triangoli aventi congruenti la base e l'altezza sono tra loro equivalenti:infatti essendo tali triangoli equivalenti a parallelogrammi sappiamo che tali parallelogrammi avendo congruente la base e l'altezza sono equivalenti Tutti i triangolo ABP sono tra loro equivalenti: basta far scorrere il punto P lungo la retta dei vertici che e' parallela alla base |

|

|

|

|