Baricentro Definiamo baricentro di un triangolo il punto di incontro delle sue mediane 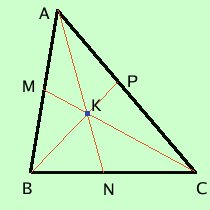Il baricentro e' il centro di massa del triangolo: se il triangolo fosse una lamina composta di sostanza omogenea il baricentro sarebbe il punto in cui puoi sospendere il triangolo senza che questo ruoti, e anche ruotando tu il triangolo questo resterebbe fisso nella nuova posizione Vale la proprieta': le tre mediane sono divise dal baricentro in due parti tli che quella che contiene il vertice e' doppia dell'altra cioe' guardando la figura si ha AK=2KN BK=2KP CK=2KM Per dimostrarlo dobbiamo usare il teorema (ingenuo) di Talete; la dimostrazione di tale teorema sara' data nel capitolo sulla similitudine; comunque cio' che ci serve e' In un fascio di rette parallele tagliato da due trasversali a segmenti congruenti sull'una corrispondono segmenti congruenti sull'altra trasversale Sarebbe a dire che la parallela alla base dal punto medio di un lato passa per il punto medio dell'altro lato si chiama teorema ingenuo di Talete perche' e' una parte del teorema di Talete completo ipotesi    AM = MB    AP = PC    BN = NC    tesi    CK = 2KM    Le due mediane BP ed AN si incontrino nel punto K. 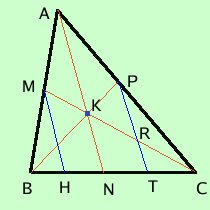Dai punti M e P mando le parallele alla mediana AN Per il teorema di Talete applicato al triangolo ABN avro' BH = HN Per il teorema di Talete applicato al triangolo ANC avro' NT = TC Essendo i segmenti BN ed NC congruenti per ipotesi avro' BH = HN = NT = TC Se ora considero il triangolo CMH avremo sempre per Talete che CR = RK = KM e quindi CK = 2KM come volevamo Attenzione: questo fatto del baricentro che divide la mediana in parti una doppia dell'altra viene spesso usato nei problemi, quindi e' un fatto da ricordare assolutamente