|
Definiamo ortocentro di un triangolo il punto di incontro delle sue altezze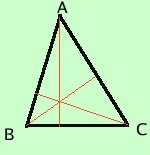 
Dimostriamo che le tre altezze passano per lo stesso punto Dai vertici del triangolo ABC mando le parallele ai lati opposti I punti A,B e C diventano i punti medi dei lati del triangolo EFG.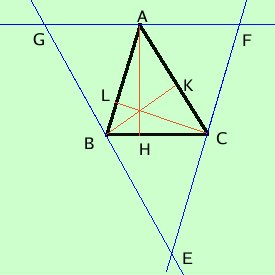 
Infatti ad esempio
consideriamo il parallelogramma ABCF, avremo BC congruente ad AF;consideriamo poi il parallelogramma GBCA, avremo BC congruente a GA; per la proprieta' transitiva avremo GA = AF cioe' A e' il punto medio del lato GF Lo stesso discorso possiamo fare per i punti B e C; quindi le tre altezze del triangolo ABC diventano i tre assi dei lati del triangolo EGF e, di conseguenza, si incontrano in uno stesso punto, come volevamo |
|
|
|
|