esercizio Data la parabola y= -x2 + 6x trovare le equazioni delle tangenti condotte alla parabola dal punto A(-2,0) e determinarne i punti di tangenza Soluzione: 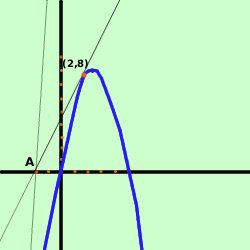prima disegniamo la parabola ed il punto A(-2,0) considero il fascio di rette passante per il punto A(-2,0) y- 0 = m(x+2) y = mx + 2m Faccio il sistema fra il fascio di rette e la parabola y = mx - 4m y= -x2 + 6x Sostituisco il valore della y dalla prima equazione nella seconda ed ottengo l'equazione risolvente mx + 2m = -x2 + 6x x2 - 6x + mx + 2m = 0 ordino x2 - x(6-m) + 2m = 0 questa e' l'equazione risolvente il sistema: per avere due soluzioni coincidenti devo porre il delta dell'equazione uguale a zero = b2-4ac = 0 Ho a = 1       b = -6+m       c = 2m = b2-4ac = (-6+m)2 - 4 (1)(2m) =0 36 - 12m + m2 - 8m = 0 metto in ordine m2 - 20m + 36 = 0 risolvo l'equazione di secondo grado ed ottengo m1 = 2 m2 = 18 Ho quindi le due tangenti Prima tangente y = 2x + 4 Seconda tangente y = 18x + 36 Ora devo trovare i punti di tangenza: e' sufficiente risolvere il sistema tangente-parabola primo sistema y = 2x + 4 y= -x2 + 6x y = 2x + 4 2x + 4 = -x2 + 6x ---------------- x2 - 6x + 2x + 4 = 0 ---------------- x2 - 4x + 4 = 0 ---------------- (x-2)2 = 0 essendo la tangente la soluzione e' doppia (delta uguale a zero e si tratta di un quadrato perfetto) y = 2x + 4 (x-2) = 0 y = 2(2) + 4 x = 2 y = 8 x = 2 il primo punto e' (2,8) secondo sistema y = 18x + 36 y= -x2 + 6x y = 18x + 36 18x + 36 = -x2 + 6x ---------------- x2 - 6x + 18x + 36 = 0 ---------------- x2 + 12x + 36 = 0 ---------------- (x+6)2 = 0 essendo la tangente la soluzione e' doppia (delta uguale a zero e si tratta di un quadrato perfetto) y = 18x + 36 (x+6) = 0 y = 18(-6) + 36 x = -6 y = 72 x = -6 il secondo punto e' (-6,72) Naturalmente e' fuori grafico