Fascio di circonferenze tangenti In questo caso le due circonferenze di base sono tangenti alla stessa retta e quindi tra loro e, di conseguenza, hanno due punti coincidenti in comune Anche qui vediamo un esercizio completo Dato il fascio di circonferenze tangenti: (1+k)x2 + (1+k)y2 + 2(k-4)x + 2(2-3k)y +2(1+k) = 0 mostrare che l'asse radicale e' la retta tangente comune alle due circonferenze di base Prima separiamo i termini contenenti il parametro da queli non contenenti il parametro x2 + kx2 + y2 +ky2 + 2kx -8x +4y -6ky +2 +2k = 0 x2 + y2 - 8x +4y +2 + k(x2 + y2 +2x -6y +2) = 0 Abbiamo quindi le due circonferenze di base x2 + y2 - 8x +4y +2 = 0 x2 + y2 +2x -6y +2 = 0 Per mostrare che l'asse radicale e' la tangente comune alle due circonferenze troviamo l'asse radicale, poi facciamo il sistema prima con una circonferenza e poi con l'altra: troveremo solo un punto (due punti coincidenti comuni) essendo il delta del sistema uguale a zero per la condizione di tangenza Calcolo l'asse radicale sottraendo fra loro le due equazioni membro a membro x2 + y2 - 8x +4y +2 = 0 x2 + y2   -2x -6y +2 = 0             -10x + 10y     = 0 Posso dividere per 10 ed ottengo l'equazione dell'asse radicale -x + y = 0 y = x    (Bisettrice del primo e terzo quadrante) Quindi, risolviamo i sistemi per mostrare che vale la condizione di tangenza nello stesso punto ed alla stessa retta 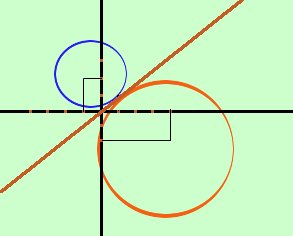y = x x2 + y2 +2x -6y +2 = 0        Calcoli e trovo come risultato un solo punto, cioe' due punti coincidenti (il delta del sistema e' uguale a zero), essendo il punto trovato il punto di tangenza T(1;1) y = x x2 + y2 - 8x + 4y +2 = 0        Calcoli e trovo come risultato un solo punto, cioe' due punti coincidenti (il delta del sistema e' uguale a zero), essendo il punto trovato il punto di tangenza T(1;1) Quindi l'asse radicale y = x e' la tangente comune alle due circonferenze base del fascio nello stesso punto T(1;1)