|
In questo caso le due circonferenze di base non hanno punti comuni fra loro. Chiameremo sempre asse radicale la retta (a1 -a2)x + (b1 - b2)y + c1 - c2= 0 e la congiungente i centri di due circonferenze del fascio saranno sempre perpendicolari a questa retta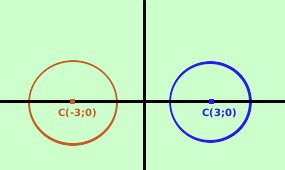 
Facciamo un esempio semplice: consideriamo il fascio di circonferenze (1+k)x2 + (1+k)y2 + 6(k-1)x + 5(1-k) = 0 Sviluppo x2 + kx2 + y2 +ky2- 6x + 6kx +5 + 5k = 0 Raccolgo i termini senza la k ed i termini con la k x2 + y2 - 6x + 5 + k(x2 + y2 + 6x + 5) = 0 le circonferenze base del fascio sono: x2 + y2 - 6x + 5 = 0 Circonferenza blu: e' la circonferenza di centro (3;0) e raggio 2 x2 + y2 + 6x + 5 = 0 Circonferenza rossa: e' la circonferenza di centro (-3;0) e raggio 2 L'asse radicale e' la retta x = 0 cioe' l'asse delle y |
|
|
|
|