Fascio di circonferenze concentriche Quando il parametro si trova solamente nel termine noto allora avremo un fascio di circonferenze concentriche L'equazione di un fascio di circonferenze concentriche si puo' ridurre a x2 + y2 + ax + by + k = 0 Infatti al variare di k varia il raggio della circonferenza mentre non variano le coordinate del centro Notiamo che, dividendo i termini con parametro da quelli senza parametro il fascio ha una sola circonferenza di base, mentre l'altra e' rappresentata da una costante. L'asse radicale stavolta si riduce ad un punto: il centro della circonferenza di bas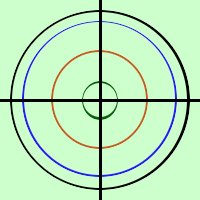e Come esempio consideriamo il fascio di circonferenze concentriche con centro l'origine x2 + y2 + k = 0 Che possiamo anche scrivere x2 + y2 = r2 Essendo r il raggio della circonferenza Da notare, nella prima equazione, che, per la realta' della circonferenza (condizione sul raggio), il termine k puo' assumere solamente valori negativi (-oo<k<0)