|
Conoscendo le coordinate di due punti nel piano e' possibile determinare le coordinate del loro punto intermedio (punto medio del segmento) Consideriamo i punti nel piano A = (x1, y1) B = (x2, y2) Inoltre chiamo M = (xM, yM) il loro punto di mezzo 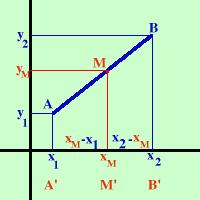 Per comodita' supponiamo che i punti si trovino nel primo quadrante, la formula che otterremo sara' comunque valida in tutto il piano Da A , B e M traccio le coordinate Sull'asse x le proiezioni saranno A' , B' e M' Poiche' M e' il punto di mezzo fra A e B allora anche M' sara' il punto di mezzo fra A' e B' Per il Teorema di Talete essendo le verticali fra loro parallele quindi A'M' =M'B' Sostituendo le misure xM - x1 = x2 - xM devo ricavare xM xM + xM = x1 + x2 2xM = x1 + x2 x1 + x2 xM = -------------- 2 Come ho trovato il punto medio sulle x posso trovarlo sulle y y1 + y2 yM = -------------- 2 Riepilogando M = ( (x1 + x2)/2 , (y1 + y2)/2 ) Il punto medio di un segmento di estremi dati e' dato dalla semisomma delle coordinate omonime degli estremi stessi Esempio: trovare il punto medio del segmento di estremi A(2,3) e B(4,7) xM = (2 + 4)/2 = 6/2 =3 yM = (3 + 7)/2 = 10/2 =5 quindi M(3,5) Vediamo ora qualche esercizio |

|

|

|

|