Punto che divide un segmento in un rapporto assegnato Conoscendo le coordinate di due punti nel piano e' possibile determinare le coordinate di un loro punto intermedio che divida il segmento secondo un rapporto assegnato m/n E' un argomento che solo molto raramente ho visto fare nelle scuole medie superiori Consideriamo i punti nel piano A = (x1, y1)       B = (x2, y2)       Inoltre chiamo P = (xk, yk) il punto che divide il segmento nel rapporto k=m/n AP      m ---- = ---- PB      n 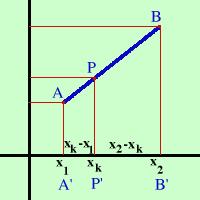Per comodita' supponiamo che i punti si trovino nel primo quadrante, la formula che otterremo sara' comunque valida in tutto il piano Da A , B e P traccio le coordinate Sull'asse x le proiezioni saranno A' , B' e P' Poiche' P e' il punto fra A e B che divide il segmento nel rapporto m/n allora anche P' dividera' il segmento A' B' nello stesso rapporto ( Teorema di Talete). Quindi A'P'       m ----- = ---- P'B'       n Sostituendo le misure xk - x1       m -------- = --- x2 - xk       n faccio il minimo comune multiplo (o equivalentemente moltiplico in croce) n(xk - x1) = m(x2 - xk) moltiplico nxk - nx1 = mx2 - mxk devo ricavare xk quindi porto i termini che lo contengono prima dell'uguale nxk + mxk = nx1 + mx2 raccolgo xk xk(n + m) = nx1 + mx2 risolvendo rispetto a xk trovo la formula finale          nx1 + mx2 xk = -------------            n + m in modo equivalente trovero' la formula per la coordinata y          ny1 + my2 yk = -------------            n + m vediamo un semplice esercizio