Volumi di solidi di rotazione Di solito ai licei scientifici questo e' l'ultimo argomento sugli integrali anche perche' il tempo a disposizione per la preparazione degli esami non basta mai, quindi tutta la parte successiva dell'analisi (integrali curvilinei, integrali doppi, tripli, ecc) viene trattata solamente nel biennio universitario e non fara' parte di questo corso (almeno per ora); 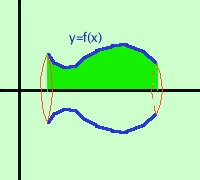Il problema che vogliamo risolvere e' come trovare il volume di un solido ottenuto dalla rotazione dell'area compresa fra una curva e l'asse delle x. Nella figura qui a fianco vorremmo trovare il volume di quella specie di vaso rovesciato ottenuto ruotando l'area compresa fra la curva y=f(x) e l'asse delle x (quella marcata in verde). La formula che utilizzeremo sara' v = [f(x)]2 dx In pratica significa che per ogni punto della funzione tracci la verticale f(x) e poi trovi l'area del cerchio di raggio f(x) con la formula r2, poi facendo l'integrale sommo tutte le aree dei cerchi ed ottengo il volume; essendo una costante lo estraggo dall'integrale Come esempio troviamo 1)   il volume del cilindro: 2)   il volume del cono: 3)   il volume della sfera: