|
Discutiamo in questa pagina il caso in cui l'area della regione di piano sia illimitata, il che non vuol dire che sia infinita.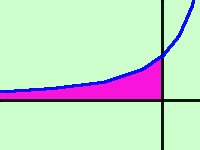 
Vogliamo calcolare l'area della regione di piano compresa fra la curva y = ex e l'asse delle x da meno infinito sino al punto zero L'area da trovare e' quella in viola; useremo questa proprieta' che applicheremo ogni volta che avremo un'area illimitata  f(x) dx = limb->  f(x) dx = limb-> F(x) = limb->F(b) - F(a)
Cioe'se abbiamo un integrale sino ad infinito (od anche sino ad un punto dove la funzione non e' definita) bastera' fare prima l'integrale e successivamente fare il limite della funzione ottenuta Quindi nel nostro caso faremo  ex dx = lima-> - ex dx =
siccome l'integrale di ex vale sempre ex avremo: = lima-> -
ex =
e0 - lima-> -ea
= 1 - 0 = 1 Qualche testo, quando non c'e'possibilita' di errore invece di fare il limite usando la lettera a o b preferisce usare la x; teoricamente sarebbe un errore anche se non cambia nulla nel risultato Quindi l'area cercata vale 1 Nota: da un lato abbiamo la funzione ex che si avvicina all'asse x in modo asintotico, cioe' dopo centinaia di chilometri ancora non tocca l'asse delle x; se vado a calcolare la distanza tra la funzione e l'asse x dopo soli 100 metri vedo che vale
Per questo non c'e' da meravigliarsi se l'area totale vale una unita' quadrata di misura del piano Se ci pensi bene quest'esempio ti fa anche vedere l'abisso che c'e' fra la matematica come scienza esatta e le scienze applicate Vediamo ora alcuni esercizi: 1) Calcolare l'area della regione di piano compresa fra la curva y=1/x e l'asse delle x tra gli estremi 0 ed 1 soluzione soluzione |
|
|
|
|