esercizio Calcolare l'area della regione di piano compresa fra la curva y=1/(x2) e l'asse delle x da 1 a piu' infinito 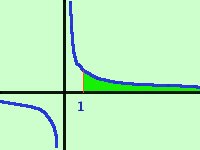Facciamo la rappresentazione grafica dell'area cercata ricordando che la funzione y=1/(x)2 e' come l'iperbole dell'esercizio precedente ma con i rami che si avvicinano piu' rapidamente agli assi L'area cercata e' quella evidenziata; Sarebbe: 1 ---- dx = x2 e quindi faremo 1 lima-> + ---- dx = x2 l'integrale di 1/(x2) vale - 1/x      vedi tabella 1 = lima-> + - ----   = x 1 = lima-> + - ----   -(-1) = 0 + 1 = 1 a L'area compresa nella regione in questo caso e' finita e vale un'unita' quadrata del piano