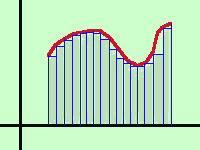
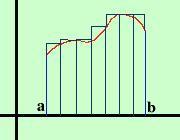Area del trapezoide Aumento il numero di intervalli in cui e' divisa la base del mio trapezoide, in questo modo l'area dei rettangoli si avvicina all'area del trapezoide f(xk)·(xk - xk-1) Area del trapezoide Per essere sicuro di individuare bene l'area del trapezoide considero anche i rettangoli che ottengo considerando come altezza il massimo della funzione nell'intervallo, in questo modo ottengo dei rettangoli esterni e la somma dei rettangoli e' superiore all'area del trapezoide. Indico con F(xk) il massimo della funzione nell' intervallo xk - xk-1, allora avro' F(xk)·(xk - xk-1) Area del trapezoide Aumento il numero di intervalli in cui e' divisa la base del mio trapezoide e li faccio diventare infiniti in modo che l'area dei rettangoli diventi uguale all'area del trapezoide, per fare questo dovremo fare il limite delle somme precedenti per n tendente ad infinito, quindi ci avvicineremo all'area da valori superiori e da valori inferiori e l'area viene ben determinata limn-> F(xk)·(xk - xk-1) = Area = limn-> f(xk)·(xk - xk-1)