Razionalizzazione con una radice di indice superiore a due al denominatore
Facciamo un esempio pratico
per vedere la regola generale
Razionalizzare
| a |
|
| -------- |
= |
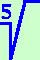 b3 b3 |
|
per togliere la radice sotto devo trasformare il denominatore in una potenza uguale all'indice della radice, in questo caso 5, cosa che posso ottenere moltiplicandolo per
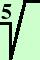 b2 pero' per non variare di valore l'espressione dovro' moltiplicare per b2 pero' per non variare di valore l'espressione dovro' moltiplicare per 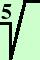 b2 anche al numeratore (in questo modo sara' come moltiplicare per 1 e il valore dell'espressione non varia) b2 anche al numeratore (in questo modo sara' come moltiplicare per 1 e il valore dell'espressione non varia)
|
a |
|
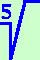 b2 b2 |
|
| = |
-------- |
· |
-------- |
= |
|
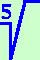 b3 b3 |
|
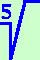 b2 b2 |
|
Ottengo
|
a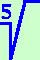 b2 b2 |
|
| = |
------- |
= |
|
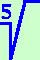 b5 b5 |
|
e semplificando la radice con la potenza ottengo il risultato
|
a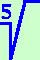 b2 b2 |
| = |
------ |
|
b |
In pratica devi moltiplicare sopra e sotto per una radice con lo stesso indice e il termine dentro (radicando) deve avere potenza uguale alla differenza fra l'indice di radice e la potenza del radicando dato:
cioe' se hai radice dodicesima di x elevato alla settima devi moltiplicare per radice dodicesima di x elevato alla quinta:
cinque = dodici meno sette
|



