.

Variabile aleatoria Veramente si dovrebbe chiamare funzione aleatoria cioe' funzione dipendente dal caso, dal verificarsi o meno di determinati eventi, ma, per ragioni storiche, ormai il termine e' entrato nell'uso comune ed e' universalmente accettato. Definizione: La variabile aleatoria e' una variabile che puo' assumere determinazioni diverse in corrispondenza di altrettanti eventi che costituiscono una partizione dello spazio delle probabilita' Vediamo su un esempio gia' fatto: 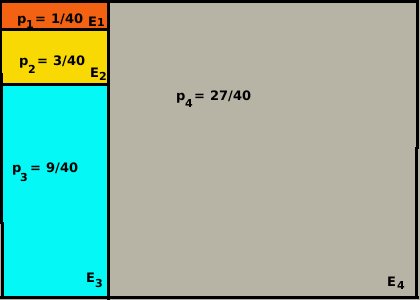estrarre una carta da un mazzo di 40 consideriamo gli eventi E1 uscita dell'asso di denari e vincita di 21 euro (1 carta) E2 uscita di un asso diverso dall'asso di denari e vincita di 1 euro (3 carte) E3 uscita di una carta di denari diversa dall'asso ne' vincita ne' perdita (9 carte) E4 uscita di una diversa dalle precedenti perdita di 1 euro (27 carte) le probabilita' sono p1 = probabilita' di uscita dell'asso di denari = 1/40 p2 = probabilita' di uscita di asso non di denari = 3/40 p3 = probabilita' di uscita di carta di denari non asso = 9/40 p4 = probabilita' di uscita di una carta diversa dalle precedenti = 27/40 Nella partizione delllo spazio delle probabilita' negli spazi degli eventi E1, E2, E3 ed E4 ho indicato i rispettivi valori delle probabilita' degli eventi considerati (valori della variabile aleatoria) In pratica la variabile (funzione) aleatoria px = f(Ex) e' la funzione che associa ad ogni evento di una partizione un numero reale (probabilita' dell'evento) Nell'esempio sopra indicato abbiamo che i valori della variabile aleatoria px = f(Ex) sono f(E1) = p1 = 1/40 f(E2) = p2 = 3/40 f(E3) = p3 = 9/40 f(E4) = p4 = 27/40 Da notare che lavoriamo su una partizione dello spazio degli eventi e quindi la somma di tutte le probabilita' deve sempre dare come risultato 1 1/40 + 3/40 + 9/40 + 27/40 = 40/40 = 1 D'ora in avanti chiamiamo la variabile aleatoria F(Xi) invece di F(Ei) in modo da richiamare il suo significato di funzione Possiamo utilizzare un metodo per rappresentare la variabile aleatoria (distribuzione della variabile aleatoria) 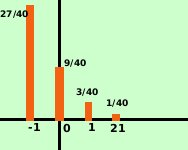X    X1 X2 X3 ......... Xn f    p1 p2 p3 ......... pn Nell'esempio precedente legando agli eventi il numero di carte che corrispondono all'evento avremo X 21 1 0 -1 f    1/40 3/40 9/40 27/40 Naturalmente i numeri sull'asse orizzontale della figura a destra non corrispondono ad una distanza ma solamente alla denominazione dell'evento. E' preferibile mettere in ordine crescente il valore della somma persa o vinta: -1, 0, +1, +21 (vedi il gioco gia' sviluppato in fondo alla pagina del capitolo precedente) Se vuoi vedere un altro esercizio Altro esempio: Consideriamo le probabilita' di uscita della faccia di un dado E1 uscita del punteggio 1 E2 uscita del punteggio 2 E3 uscita del punteggio 3 E4 uscita del punteggio 4 E5 uscita del punteggio 5 E6 uscita del punteggio 6 le relative probabilita' sono p1 = probabilita' di uscita del punteggio 1 = 1/6 p2 = probabilita' di uscita del punteggio 2 = 1/6 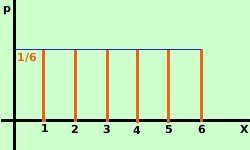p3 = probabilita' di uscita del punteggio 3 = 1/6 p4 = probabilita' di uscita del punteggio 4 = 1/6 p5 = probabilita' di uscita del punteggio 5 = 1/6 p6 = probabilita' di uscita del punteggio 6 = 1/6 possiamo usare la rappresentazione X 1 2 3 4 5 6 f   1/6 1/6 1/6 1/6 1/6 1/6