Conseguenze
Dai postulati deriva che:
- 1= P(S) = P( S
 Ø ) = P(S) +
P(Ø)
Quindi P(Ø) = 0
La probabilita' dell'evento impossibile e' nulla
- Dato un qualunque insieme A appartenente ad S abbiamo
1= P(S) = P( A A_) = P(A) + P(A_)
Quindi, ricavando P(A) ho: P(A) = 1 - P( A_)
La
probabilita' di un evento e' uguale ad 1 meno la probabilita'
dell'evento contrario
- Essendo P(A) + P(A_) = 1
ne segue che
0  P(A) 1
La probabilita' di un evento e' sempre compreso
fra 0 ed 1
- se A
 B allora
P(A) P(B)
Se A e' contenuto in B allora la probabilita'
dell'evento A e' minore della probabilita' dell'evento B (e'
uguale se A=B)
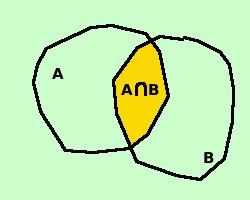
- se
A e B sono due eventi qualsiasi si ha sempre
P(A B) = P(A) + P(B) - P(A  B)
Infatti se considerassi solo P(a) e P(B)
considererei due volte la parte comune A  B
Esempio:
Calcolare la probabilita' di estrarre da un mazzo di quaranta carte una carta di
denari oppure una figura:
Evento A: estrazione di una carta di denari
Evento B: estrazione di una figura
Le carte di denari sono 10 P(A)= 10/40 = 1/4
Le figure sono 12 P(B) = 12/40 = 3/10
Le carte che sono contemporareamente figure e denari sono 3 P(AB)= 3/40
quindi: P = P(A)+P(B)-P(AB) = 10/40 + 12/40 - 3/40 =
19/40 ~ 0,475 = 47,5%
| .
