|
Utilizzando la relazione di equivalenza e' possibile generare logicamente, mediante gli insiemi, l'insieme N dei Numeri Naturali : 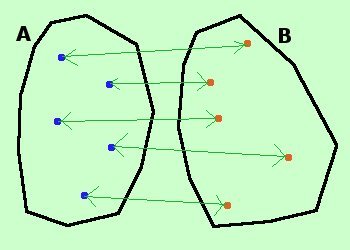
Per poterlo mostrare ti anticipo la nozione di corrispondenza biunivoca fra due insiemi Una corrispondenza biunivoca fra due insiemi si ha quando ad ogni elemento del primo insieme corrisponde uno ed un solo elemento del secondo insieme e viceversa Considero l'insieme di tutti gli insiemi e considero la relazione "e' in corrispondenza biunivoca" la relazione e' di equivalenza: infatti e' contemporaneamente
Questa relazione divide l'insieme di tutti gli insiemi in gruppi (classi) tali che tutti gli elementi della stessa classe hanno la stessa quantita' di elementi (cardinalita') e quindi l'insieme quoziente, essendo formato da tutti gli insiemi con lo stesso numero di elementi puo' essere rappresentato da un numero cioe' otteniamo l'insieme N dei numeri naturali: 1, 2, 3, 4, 5, 6, 7, .......... 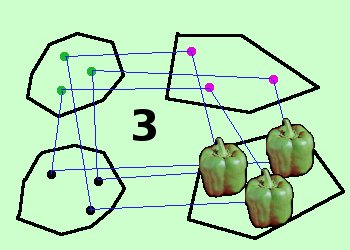
quindi, ad esempio, il numero 3 rappresentera' la classe formata da tutti gli insiemi composti da 3 elementi |

|

|

|

|