Corrispondenza biunivoca Diremo che un'applicazione f : A --> B e' una corrispondenza biunivoca (od un applicazione biiettiva ) se e' contemporaneamente Iniettiva Suriettiva f : A su > B 1-1 Cioe' ad ogni elemento di A corrisponde un elemento di B e viene esaurito l'insieme B In pratica significa che ad ogni elemento di A corrisponde un solo elemento di B e ad ogni elemento di B corrisponde un solo elemento di di A, cioe' la relazione e' iniettiva sia da A a B che a rovescio da B ad A (si dice biiettiva) 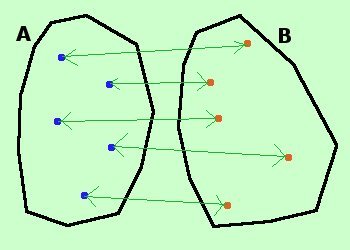esempio di corrispondenza biunivoca: ogni elemento di A e' collegato con un solo elemento di B e l'insieme B viene esaurito (od anche ogni elemento di B e' collegato con un solo elemento di A) Un esempio abbastanza semplice di corrispondenza biunivoca in un' aula scolastica e' quello fra ogni alunno della classe ed il suo banco: ad ogni alunno corrisponde il suo banco e ad ogni banco corrisponde il suo alunno; la corrispondenza non e' biunivoca il giorno che l'alunno Pierino marina la scuola mentre e' biunivoca quando tutti gli alunni sono presenti In matematica la corrispondenza biunivoca e' importantissima perche' tutte le proprieta' matematiche di un insieme A sono valide anche in tutti gli insiemi che possono essere messi in corrispondenza bunivoca con A; Come dicevo ai miei alunni: "E' come se invece di promuovere voi si promuovessero i vostri banchi" Qualcuno la chiama anche biiezione (termine orrendo!)