Partizione di un insieme Quando il ricoprimento finito e' formato da insiemi senza elementi comuni allora avremo una partizione dell'insieme E 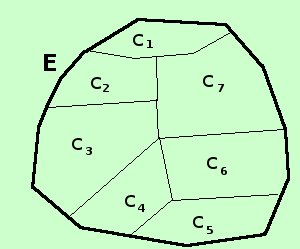Diremo che un insieme finito di sottoinsiemi non vuoti dell'insieme E e' una partizione dell'insieme E se ogni elemento di E appartiene ad uno ed uno solo dei sottoinsiemi Diamo ora la definizione matematica: Definizione: Si dice che si opera una partizione dell'insieme E nelle classi (sottoinsiemi) C1, C2, C3, ......., Cn se tali classi godono delle seguenti proprieta' nessuna classe e' vuota Ci Ø tutte le classi sono disgiunte fra loro Ci Cj = Ø L'unione di tutte le classi restituisce l'insieme E i=1 i=n Ci = E Vediamo un semplice esempio: sia E = { 1, 2, 3, 4, 5, 6} una partizione dell'insieme E (tra quelle possibili) potrebbe essere costituita dagli insiemi (classi) C1   C2   C3 C1 = { 1, 2, 3} C2 = { 4} C3 = { 5, 6 }