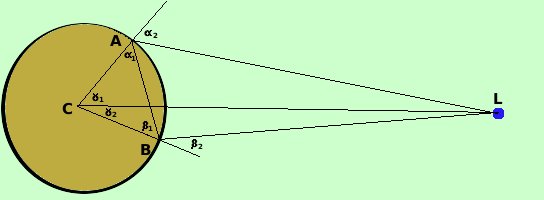
Distanza terra luna Ormai l'argomento e' non piu' d'attualita: se vuoi misurare la distanza terra-luna oggi basta usare un raggio laser e misurare il tempo che impiega per esere riflesso verso l'osservatore: ottieni una misura con una precisione sbalorditiva. Quando gli astronauti sono sbarcati sulla luna hanno lasciato uno specchio appositamente per questo Comunque storicamente questi calcoli hanno avuto la loro importanza e quindi conviene conoscerli: qui misuriamo la distanza fra i centri della terra e della luna Consideriamo due punti A e B sulla superficie terrestre e sullo stesso meridiano, per semplicita' da parti opposte rispetto all'equatore terrestre; Conosciamo: Il valore del raggio terrestre AC e BC il valore dell'angolo ACL = 1 (latitudine di A) il valore dell'angolo BCL = 2 (latitudine di B) il valore degli angoli CAB = CBA = 1 = 1 = (180° - 1 -2): 2 Il triangolo ACB e' isoscele avendo come lati due raggi della sfera terrestre (effettivamente la terra non e' sferica, comunque, per noi che studiamo la distanza per ragioni storiche, e' sufficiente considerarla sferica) Misuriamo inoltre L'angolo 2 declinazione della luna rispetto alla verticale Considero il triangolo LCB: so che l'angolo LBC = 180° - 2 inoltre l'angolo BLC =180°- (2 + 180° - 2) = 2 - 2 puoi anche osservare che 2 e' esterno al triangolo LCB mentre 2 e' interno e non adiacente: allora l'altro angolo interno e non adiacente vale 2 - 2 Quindi conosco due angoli ed un lato e posso risolverlo: Applico il teorema dei seni LC ------------------- sen (180° - 2) AC =  ---------------------------    sen (2 - 2) e, per la relazione sugli angoli supplementari LC ------------ sen 2 AC =  ---------------------------    sen (2 - 2) Quindi otteniamo LC = AC sen 2  --------------    sen (2 - 2) Per esercizio puoi ripetere la misura per una latitudine sopra l'equatore (punto A) oppure puoi calcolare la distanza fra il punto B (superficie della terra) e la luna