|
Veramente io non ho mai visto costruire una torre per metterla in una depressione, ma consideriamo solo come un esempio di tipo matematico 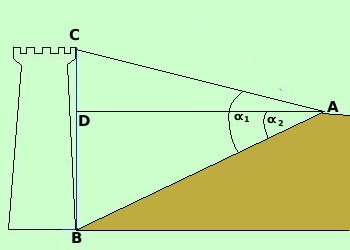 Conosciamo
ConosciamoLa distanza AB L'angolo L'angolo possiamo misurare AB con un decametro a nastro e gli angoli mediante il teodolite L'angolo CAD vale Essendo il triangolo ACD rettangolo avremo che l'angolo ACD=90°- ( Se ora considero il triangolo ABC conosco: la distanza AB l'angolo BAC = l'angolo ACD=90°- ( Quindi conoscendo due angoli ed un lato posso risolvere il triangolo: applico il teorema dei seni per trovare la misura di BC
Esercizio: supponiamo di spostarci dal punto B di 30 metri AB = 30 m e che l'angolo di visuale e l'angolo di elevazione e quindi ho
|