 Consideriamo nel primo quadrante l'angolo
Consideriamo nel primo quadrante l'angolo
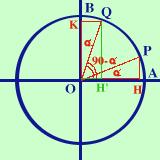
L'angolo che resta tra (90° - Se io considero come origine degli archi B ho che il triangolo OQK e' il triangolo con lati il seno ed il coseno Se io considero come origine degli archi A ho che il triangolo OPH e' il triangolo con lati il seno ed il coseno Essendo gli angoli ( Se considero l'angolo (90° - Quindi osservando l'uguaglianza dei lati posso scrivere QH' = OH cioe' sen(90° - OH' = PH cioe' cos(90° - Cioe' Due angoli complementari (la cui somma e' 90°) scambiano fra loro il seno ed il coseno Applicando la seconda relazione fondamentale avrai poi che tang(90° - cotg(90° - |

|

|

|

|